Python实现二叉树的前中后序遍历

本文主要说一下利用python实现二叉树的前中后序遍历的方法，和实现原理以及方法， 树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。

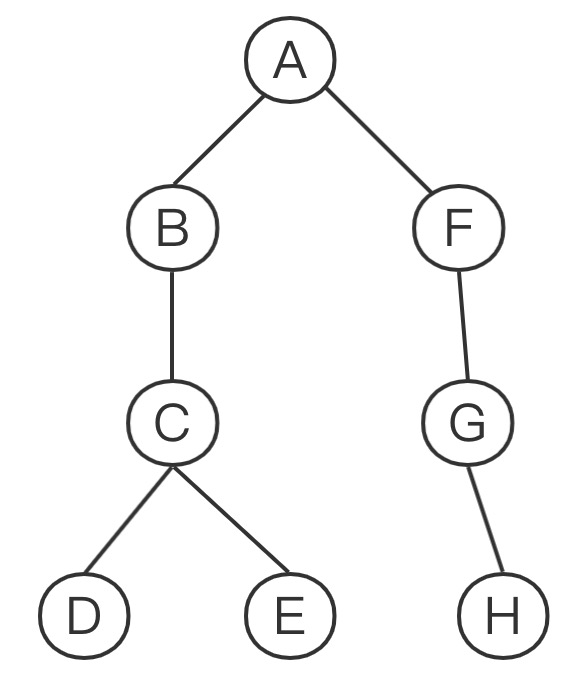
二叉树的结构

前中后序遍历对应的规则：

先序遍历

先序遍历的原则是：先根、再左、再右。
即：ABCDEFGH

中序遍历

中序遍历的原则是：先左、再根、再右。
即：BDCEAFHG

后序遍历

后序遍历的原则是：先左、再右、再根。
即：DECBHGFA

# 首先定义树的根节点
class Node(object):
    """docstring for Node"""
 
    def __init__(self, elem=0, left=None, right=None):
        self.elem = elem
        self.lchild = left
        self.rchild = right
 
 
# 定义一棵二叉树
class BinaryTree(object):
    """docstring for BinaryTree"""
 
    def __init__(self):
        # 根节点
        self.root = None
 
    def add(self, item):
        # 向树中插入元素, 使用队列存储元素, 读取与弹出
        node = Node(item)
        if self.root is None:
            self.root = node
            return
        # 用顺序表实现队列, 先入先出FIFO
        # 首先传入根节点信息
        queue = [self.root]
 
        while queue:
            cur_node = queue.pop(0)
 
            # 若当前节点的左孩子为空, 将节点赋给当前节点左孩子
            if cur_node.lchild is None:
                cur_node.lchild = node
                return
                # 若当前节点左孩子不为空, 左孩子添加到当前节点中
            else:
                queue.append(cur_node.lchild)
 
            # 接下来同样判断右孩子
            if cur_node.rchild is None:
                cur_node.rchild = node
                return
            else:
                queue.append(cur_node.rchild)
 
    def breadth_travel(self):
        """广度遍历: 方法同add, 是一种反过来的操作
        """
        # 使用队列
        queue = [self.root]
        ret = []
        if self.root is None:
            return
        while queue:
            cur_node = queue.pop(0)
            # 打印结点值
            # print(cur_node.elem, end=" ")
            ret.append(cur_node.elem)
            if cur_node.lchild:
                queue.append(cur_node.lchild)
            if cur_node.rchild:
                queue.append(cur_node.rchild)
        print(ret)
 
    def pre_order(self, node):
        """前序遍历: 递归方法"""
        # if node is None:
        #     return
        # print(node.elem, end=" ")
        # self.pre_order(node.lchild)
        # self.pre_order(node.rchild)
        ret = []
 
        def recur_0(node):
            if node:
                ret.append(node.elem)
                recur_0(node.lchild)
                recur_0(node.rchild)
        recur_0(node)
        print(ret)
 
    def in_order(self, node):
        """中序遍历"""
        # if node is None:
        #     return
        # self.in_order(node.lchild)
        # print(node.elem, end=" ")
        # self.in_order(node.rchild)
        ret = []
 
        def recur_1(node):
            if node:
                recur_1(node.lchild)
                ret.append(node.elem)
                recur_1(node.rchild)
        recur_1(node)
        print(ret)
 
    def post_order(self, node):
        """后序遍历"""
        # 递归遍历跳出的条件
        # if node is None:
        #     return
        # self.pre_order(node.lchild)
        # self.pre_order(node.rchild)
        # print(node.elem, end=" ")
        ret = []
 
        def recur(node):
            if node:
                recur(node.lchild)
                recur(node.rchild)
                ret.append(node.elem)
        recur(node)
        print(ret)
 
    def pre_order_1(self, node):
        """前序遍历(中左右): 非递归, 需要使用栈(递归的本质是栈实现)来实现"""
        # 定义一个栈
        st = []
        # 定义顺序数组
        result_arr = []
        if node:
            st.append(node)
        while st:
            node = st.pop()
            # 中
            result_arr.append(node.elem)
            # 右
            if node.rchild:
                st.append(node.rchild)
            # 左
            if node.lchild:
                st.append(node.lchild)
        print(result_arr)
 
    def in_order_1(self, node):
        """中序遍历(左中右), 需要指针(由于遍历的节点顺序和处理的节点顺序不同)"""
        st = []
        result_arr = []
        cur_node = node
        while cur_node or st:
            if cur_node:
                # 利用指针访问结点,访问到最底层数据
                # 结点入栈
                st.append(cur_node)
                # 左
                cur_node = cur_node.lchild
            else:
                cur_node = st.pop()
                # 中
                result_arr.append(cur_node.elem)
                # 右
                cur_node = cur_node.rchild
        print(result_arr)
 
    def in_order_2(self, node):
        """中序遍历(左中右), 通解"""
        st = []
        result_arr = []
        if node:
            st.append(node)
        while st:
            node = st[-1]
            if node:
                st.pop()
                if node.rchild:
                    st.append(node.rchild)
                st.append(node)
                # 空节点入栈作为标记
                st.append(None)
                if node.lchild:
                    st.append(node.lchild)
            else:
                # 空节点出栈
                st.pop()
                node = st[-1]
                st.pop()
                result_arr.append(node.elem)
        print(result_arr)
 
    def post_order_1(self, node):
        """后序遍历(左右中), 可以直接由前序遍历得到"""
        # 定义一个栈
        st = []
        # 定义顺序数组
        result_arr = []
        if node:
            st.append(node)
        while st:
            node = st.pop()
            # 中
            result_arr.append(node.elem)
            # 左
            if node.lchild:
                st.append(node.lchild)
            # 右
            if node.rchild:
                st.append(node.rchild)
        print(result_arr[::-1])
 
    def post_order_2(self, node):
        """后序遍历(左右中), 可以直接由前序遍历得到"""
        # 定义一个栈
        st = []
        # 定义顺序数组
        result_arr = []
        while st or node:
            while node:
                st.append(node)
                # 遍历二叉树直到结点不再含有左节点(右节点)
                node = node.lchild if node.lchild else node.rchild
            node = st.pop()
            # 最后加入中结点
            result_arr.append(node.elem)
            # 判断并开始遍历右节点(node指向右节点), 然后继续进行入栈操作(while内循环)
            node = st[-1].rchild if st and st[-1].lchild == node else None
        print(result_arr)
 
 
if __name__ == '__main__':
    tree = BinaryTree()
    for i in range(9):
        tree.add(i)
    print("广度遍历: ")
    tree.breadth_travel()
    print("\n深度遍历: ")
    print("前序遍历: 递归")
    tree.pre_order(tree.root)
    print("中序遍历: 递归")
    tree.in_order(tree.root)
    print("后序遍历: 递归")
    tree.post_order(tree.root)
    print()
    print("前序遍历: 非递归")
    tree.pre_order_1(tree.root)
    print("中序遍历: 非递归")
    tree.in_order_1(tree.root)
    print("中序遍历: 非递归, 不需要指针")
    tree.in_order_2(tree.root)
    print("后序遍历: 非递归, 修改自前序")
    tree.post_order_1(tree.root)
    print("后序遍历: 非递归, 直接写")
    tree.post_order_2(tree.root)
 
"""
广度遍历: 
0 1 2 3 4 5 6 7 8 
深度遍历: 
前序遍历: 递归
0 1 3 7 8 4 2 5 6 
中序遍历: 递归
7 3 8 1 4 0 5 2 6 
后序遍历: 递归
7 8 3 4 1 5 6 2 0 
前序遍历: 非递归
[0, 1, 3, 7, 8, 4, 2, 5, 6]
中序遍历: 非递归
[7, 3, 8, 1, 4, 0, 5, 2, 6]
后序遍历: 非递归
[7, 8, 3, 4, 1, 5, 6, 2, 0]
"""

以上就是二叉树的实现方式，仅供参考，如果有更好的方式可以留言一起探讨。。。。。